¿Cuáles son los puntos de corte de una recta?

¿Cuáles son los puntos de corte de una recta?

Para encontrar el punto de corte de una recta con el eje X se puede igualar la ecuación de la recta a cero (y = f(x) = 0) lo que da como resultado una ecuación en términos de X que representa la abscisa del punto de corte. Así, si la ecuación de la recta es la explícita y=mx + n, donde m es la pendiente y n es la ordenada al origen, entonces el punto de corte con el eje X es:

Mx + n = 0  ⇒  mx = -n ⇒  x = -n/m

El punto de corte de una recta con el eje X es entonces el punto (-n/m, 0).

Para encontrar el punto de corte con el eje Y se puede simplemente evaluar la ecuación de la recta en x = 0, lo que da como resultado una ecuación en términos de Y que representa la ordenada del punto de corte. Por ejemplo, si la ecuación de la recta es la explícita y = mx + n , entonces el punto de corte con el eje Y es:

Y = m ∙ 0 + n  ⇒  y = n

El punto de corte de una recta con el eje Y es entonces el punto (0, n). Resulta interesante darse cuenta de que de aquí viene el nombre de “ordenada en el origen” para el valor n, pues indica exactamente el punto de corte con el eje de ordenadas (el eje Y).

¿Cuáles son los puntos de corte entre dos rectas?

Los puntos de corte entre dos rectas son aquellos puntos donde las dos rectas se intersecan. Como las rectas no cambian de dirección, podrán tener uno o ningún punto de corte, pero nunca dos o más. Para encontrarlo se deben seguir los siguientes pasos:

Escribir las ecuaciones de las dos rectas en la forma explícita y = mx + n:

R₁: y = mx + n

R₂: y = m´x + n

Igualar las dos ecuaciones para encontrar el valor de X que hace que Y sea igual en ambas ecuaciones. Esto significa que:

mx + n = m´x + n´

Resolver la ecuación para encontrar el valor de x, siendo este el valor de X del punto de corte de las dos rectas, que se complementa con el correspondiente valor de X sustituyendo en cualquiera de las rectas, obteniendo el punto de corte (x, y) de las dos rectas.

Es importante tener en cuenta que es posible que las dos rectas no se intersequen en ningún punto, siendo las dos rectas paralelas. También es posible que las dos rectas se superpongan, en cuyo caso todas las coordenadas de la recta serán puntos de corte y las rectas serán coincidentes.

¿Cuáles son los puntos de corte de una parábola?

Para encontrar los puntos de corte de una parábola con el eje X se puede igualar la ecuación de la parábola a cero (y = f(x) = 0), dando como resultado una ecuación en términos de x. Así, como la ecuación de la parábola es y = ax² + bx + c, donde a, b y c son valores reales, los puntos de corte con el eje X pueden determinarse mediante la fórmula cuadrática:

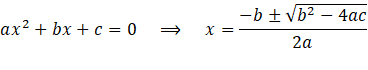
Por ello, para una parábola habrá ninguno, uno o dos puntos de corte con el eje X, dependiendo de si el término dentro de la raíz cuadrada es negativo (b² - 4ac < 0), cero (b² - 4ac = 0) o positivo (b² - 4ac > 0)

Si el término es positivo (b² - 4ac < 0) habrá dos puntos de corte:

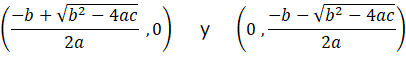
Si el término es cero (b² - 4ac = 0) habrá un solo punto de corte:

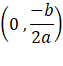
Si el término es negativo (b² - 4ac < 0) no habrá ningún punto de corte. Esta condición es equivalente a que el vértice de la parábola esté por encima del eje de coordenadas y su concavidad apunte hacia arriba, o por debajo del eje de coordenadas y su concavidad apunte hacia abajo.

Los puntos de corte de una parábola con el eje X, o lo que es lo mismo, las soluciones de su ecuación cuadrática, se denominan las raíces del polinomio de grado 2 asociado.

Para encontrar el punto de corte con el eje Y se puede simplemente evaluar la ecuación de la parábola en x=0, lo que da como resultado una ecuación en términos de Y que representa la ordenada del punto de corte. Así, como la ecuación de la parábola es y = ax² + bx +c, entonces el punto de corte con el eje Y es:

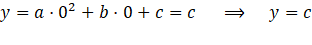
El punto de corte de una parábola con el eje Y es entonces el punto (0, c). Este valor c podría interpretarse como en el caso del valor n para la recta, como una “ordenada en el origen”.

Véase un ejemplo con la función f(x) = x² - 4x + 3:

Para encontrar los puntos de corte con el eje X, se iguala la función a cero y se resuelve con la fórmula cuadrática:

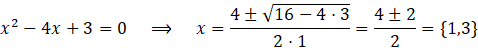
Por lo tanto, los puntos de corte con el eje X son (1, 0) y (3, 0).

Para encontrar el punto de corte con el eje Y se evalúa la función en x = 0:

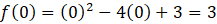
Por lo tanto, el punto de corte con el eje Y es (3, 0).

Entonces, los puntos de corte de la función f(x) = x² - 4x + 3son los puntos (1, 0), (3, 0) y (0, 3).

¿Cuáles son los puntos de corte entre dos parábolas?

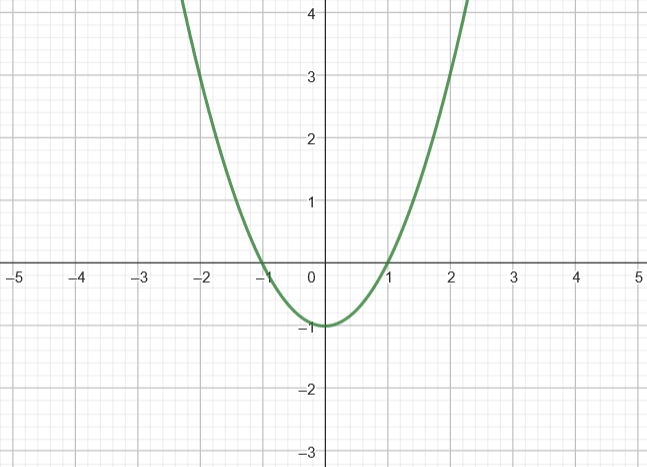
Para encontrar los puntos de corte entre dos parábolas se deben igualar sus funciones y despejar los valores que cumplen dicha condición. De manera general, para dos parábolas:

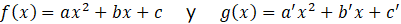
Igualando ahora sus funciones se obtiene una relación cuadrática directa que debe cumplir X:

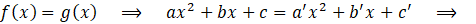
Resolviendo entonces por la fórmula general para una ecuación polinómica de grado 2 se pueden obtener las abscisas de los dos puntos de corte posibles:

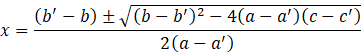
Las ordenadas de estos posibles puntos se obtienen simplemente sustituyendo en una de las funciones parabólicas.

Cabe destacar que puede haber dos, uno o ningún punto de corte entre dos parábolas:

Habrá dos puntos de corte si se cumple que el argumento de la raíz es estrictamente positivo, es decir, que (b – b´)² > 4(a – a´)(c – c´).

Habrá un único punto de corte si las parábolas son tangentes, es decir, si se da que el argumento de la raíz es 0, o lo que es lo mismo, si (b – b´)² > 4(a – a´)(c – c´). En este caso el valor X del punto de corte es simplemente:

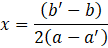
No habrá puntos de corte si el argumento de la raíz cuadrada es negativo, es decir, si (b – b´)² > 4(a – a´)(c – c´).

Por ejemplo, considerando las parábolas:

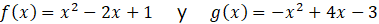
Para encontrar los puntos de corte se igualan las funciones:

Así, resolviendo la ecuación se obtienen los dos puntos de corte:

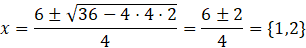
Por lo tanto, los valores de X que satisfacen la ecuación son x = 1 y x = 2. Para encontrar las coordenadas de los puntos de corte, se sustituyen los X en una de las funciones:

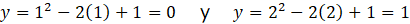
Por lo tanto, los puntos de corte son: (1, 0) y (2, 1).

¿Cuáles son los puntos de corte entre una recta y una parábola?

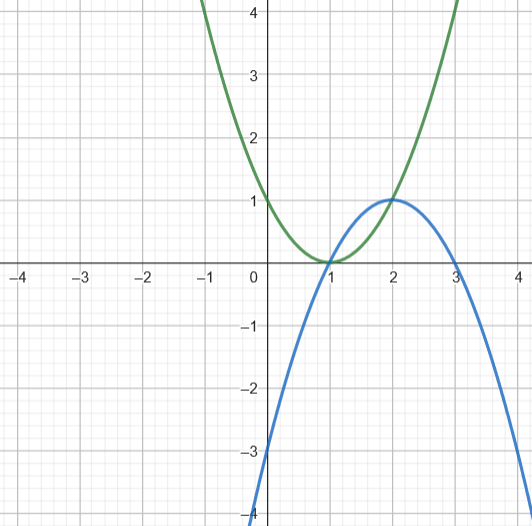
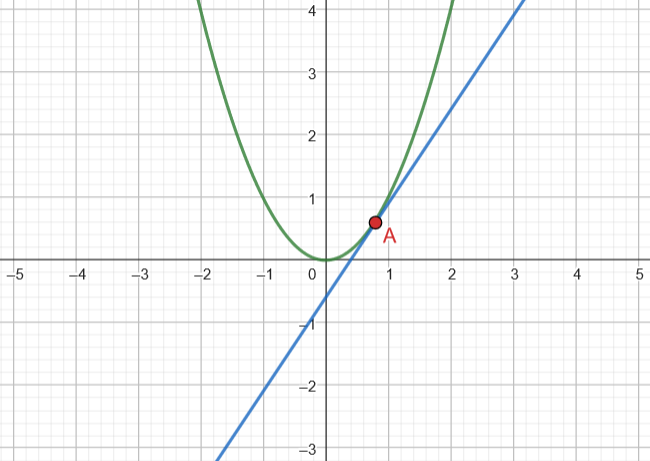
Los puntos de corte entre una parábola y una recta son los puntos en los que ambas funciones se intersecan. Para encontrar estos puntos, se deben seguir los siguientes pasos:

Escribir la ecuación de la parábola en la forma y = ax² + bx +c, donde a, b y c son constantes.

Escribir la ecuación de la recta en la forma y = mx + n, donde m y n son constantes (pendiente y ordenada en el origen, respectivamente).

Igualar las dos ecuaciones para encontrar los valores de X que hacen que Y sea igual en ambas ecuaciones. Esto es:

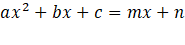
Resolver la ecuación resultante para encontrar los valores de X que la cumplen. Estos valores de X son los puntos de corte de la parábola y la recta:

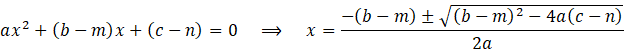
Sustituir cada valor de X encontrado en una de las dos ecuaciones para encontrar el valor correspondiente de Y. Esto da el punto de corte (x, y) de la parábola y la recta:

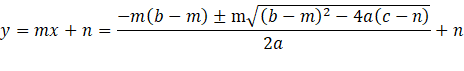
Es importante tener en cuenta que puede haber ninguno, uno o dos puntos de corte entre una parábola y una recta, que dependerá exclusivamente del valor del argumento de la raíz cuadrada:

Si es negativo, es decir, (b – m)² < 4a (c – n), entonces la parábola y la recta no se cortarán.

Si es cero, es decir, (b – m)² < 4a (c – n), entonces la parábola y la recta se tocarán en un único punto (el punto de corte). En este caso se dice que la recta es tangente a la parábola.

Si es positivo, es decir, (b – m)² < 4a (c – n), entonces habrá dos puntos de corte. 

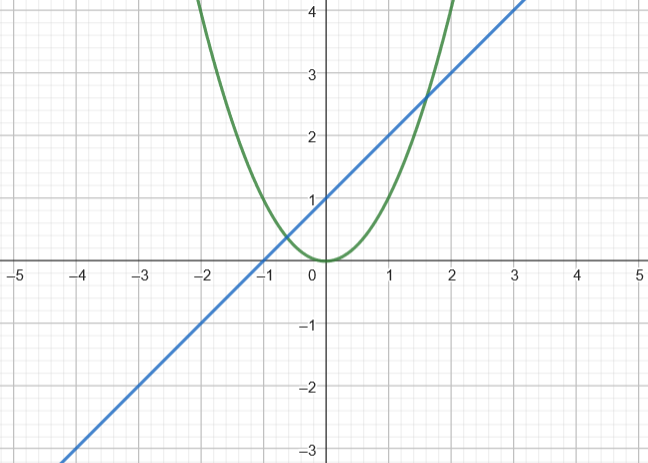
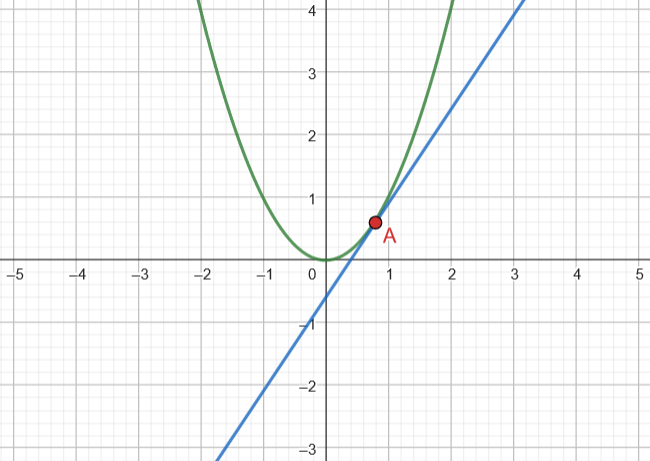
Para graficar la intersección de la parábola y la recta es clave conocer su(s) punto(s) de corte, pues se deben usar estos como referencia. Asimismo, se deberán otros puntos notables de la parábola, como su vértice, para determinar la forma de la curva. En general, la recta afectará la forma de la parábola, y su posición con respecto a la parábola determinará si hay uno o dos puntos de corte.

Resulta interesante plantearse y entender que los puntos de corte de una parábola con los ejes son en realidad los puntos de corte de una parábola con las rectas y = 0 (eje X), x=0 (eje Y):

Para el eje X: 

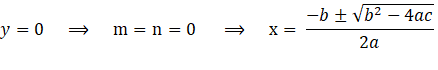
Así, se devuelve la ecuación obtenida en otras ocasiones para los puntos de corte con el eje de abscisas X de una parábola.

Para el eje Y:

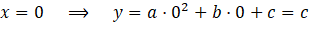
Como en el caso anterior, se recupera el punto de corte obtenido para una parábola con el eje de ordenadas Y.

¿Cuáles son los puntos de corte de una función polinómica?

De manera general, para una función polinómica de grado n definida por la ecuación: 

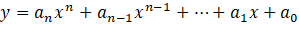
Se pueden encontrar sus puntos de corte con los ejes de coordenadas al resolver el sistema de ecuaciones formado por la ecuación del polinomio y la ecuación del eje de coordenadas (y = 0 para el eje X o x = 0 para el eje Y).

El punto de corte de la función polinómica con el eje X se obtiene resolviendo la ecuación y = f(x) = 0, que puede ser resuelta utilizando técnicas de factorización o utilizando la fórmula general si son de grado menor que 5. Como curiosidad, para ecuaciones polinómicas de grado mayor o igual que 5 no existe (ni puede existir) una fórmula para obtener sus soluciones.

El punto de corte de la función polinómica con el eje Y se puede obtener simplemente evaluando la función en x = 0, lo que da como resultado la ordenada del punto de corte. Es decir, el punto de corte de la función polinómica con el eje y es el punto (0, a₀).

De esta forma, para una función polinómica de grado n puede haber de 0 a n puntos de corte con el eje X, pero solo un punto de corte con el eje Y. Estudiando más a fondo la situación, si la función polinómica es de grado par, puede haber de 0 a n puntos de corte con el eje X, mientras que si es de grado impar debe haber al menos un punto de corte con el eje X, es decir de de 0 a n puntos de corte posibles.

Los puntos de corte de una función polinómica con el eje X, o lo que es lo mismo, las soluciones de su ecuación, se denominan las raíces del polinomio de grado n.

Desde Resueltoos te invitamos a conocer nuestro innovador método de enseñanza basado en la metodología CooRasis para desarrollar el potencial de aprendizaje de niños de todas las edades y conocimientos.

Una plataforma que ofrece un sistema interactivo de clases particulares, que  permite organizar el tiempo del alumno y los padres, dando una gran ventaja para los institutos, permitiendoles la posibilidad de aprovechar sus aulas y recursos para gestionar, también, las clases extraescolares de sus alumnos, lo que proporciona un recurso extra para entidades educativas y para el propio alumnado. Se adapta al nivel de cada uno y facilita el aprendizaje mediante material audiovisual, apuntes y ejercicios guiados. Clases, resolución de ejercicios paso a paso, gran cantidad de material audiovisual. Apuntes, y ejercicios resueltoos para que el alumno pueda seguir la materia y conseguir una evolución significativa en su aprendizaje. Ya puedes disfrutar y poner en practica este tipo de aprendizaje a través de su suscripción y de sus cursos de matemáticas, física, química, lengua, historia y dibujo técnico.

Seguir aprendiendo:

1- La inteligencia artificial chat GPT

2- ¿Quieres ser una gran científica? 

3- Puntos de corte otras funciones

4- Dominio de una función

5- Puntos de corte con los ejes