Vector unitario

VECTOR UNITARIO

Vector unitario

El vector unitario se define como un vector de módulo unidad (de módulo uno). Es muy común que se utilice la expresión “vector normal” para referirse a un vector de módulo 1. 

Este tipo de vectores son útiles para muchos casos, pero en especial para definir direcciones y sentidos. Como su módulo carece de importancia, los vectores unitarios indican una dirección y un sentido de forma explícita. Por ello, cualquier vector distinto de 0 puede expresarse y descomponerse como un producto de su módulo y de su vector unitario. Esto es:

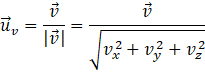
Aplicando este concepto, dado un vector

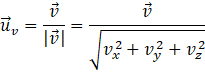
cualquiera (distinto de 0) se puede obtener su vector unitario multiplicando el vector por el inverso de su módulo, o lo que es lo mismo, dividiendo el vector por su módulo. Es decir, dado un vector

 :

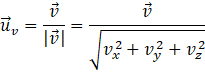Al proceso de conseguir el vector unitario de un vector cualquiera se le denomina normalización del vector. Además, el vector unitario de un vector

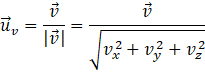
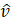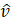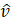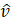se suele escribir como o con un acento circunflejo (^) en lugar de una flecha: . Por ejemplo, sea el vector de , su módulo será: 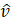. Como el módulo el distinto de 0, el vector se puede normalizar y se obtiene su vector unitario: V

La descomposición del vector será entones: R²

Se puede comprobar que, en efecto, el vector R² es unitario: R²

La representación de este vector en el espacio euclídeo bidimensional R² nos da una idea de la importancia del vector unitario y de cómo indica la dirección y sentido del vector: R²

Otro ejemplo, sea el vector R² de 

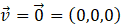
su módulo será:

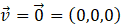
Como el módulo el distinto de 0, el vector se puede normalizar y se obtiene su vector unitario:

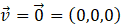
La descomposición del vector será entones:

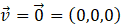
Se puede comprobar que, en efecto, el vector

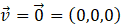
es unitario:

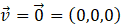
La representación de este vector en el espacio euclídeo tridimensional

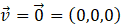
nos da una idea de la importancia del vector unitario y de cómo indica la dirección y sentido del vector:

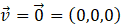
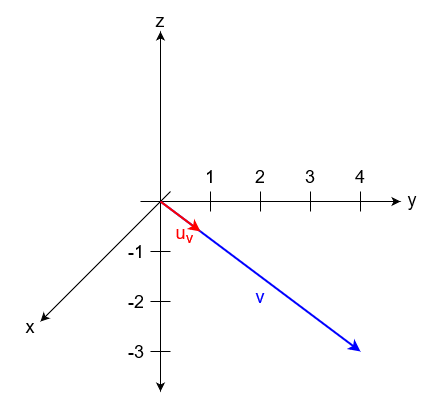
En este ejemplo se puede observar cómo el vector unitario representa perfectamente la dirección y el sentido del vector. Por ende, el vector unitario permite aplicar todas las propiedades vectoriales que no dependan del módulo.

Observación: Hay que tener mucho cuidado cuando se realizan divisiones en una operación con vectores, pues los vectores no pueden dividirse. Lo que sí se puede hacer es dividir un vector por un escalar (por un número), que equivale a multiplicar el vector por el inverso de dicho escalar.

Se puede comprobar que la definición de vector unitario carece de sentido cuando se trata de vectores nulos (V=0=(0, 0, 0)), pues su módulo sería 0 y no podría dividirse por él. Además, un vector nulo no tiene ni dirección ni sentido, por lo que el “vector unitario” asociado a él no aportaría ninguna información.

Base de vectores unitarios

Los vectores unitarios son claves en la formación de bases de espacios vectoriales. Cuando se habla de una base de un espacio vectorial se entiende un conjunto finito (o numerable) de vectores de dicho espacio que puede generar el espacio. Así, cada vector del espacio podría escribirse como una combinación lineal de los vectores de la base.

Un conjunto de vectores que forman una base de un espacio vectorial se denomina sistema generador de dicho espacio vectorial, y existirán infinitas posibles, pues cualquier conjunto linealmente independiente de d vectores será una base válida (d es la dimensión del espacio vectorial). Por ello, interesa saber qué base es la más apropiada.

Las bases óptimas para representar un espacio vectorial son bases ortonormales, es decir, bases formadas por vectores unitarios linealmente independientes y que son todos perpendiculares entre sí. Si los vectores no son unitarios (no tienen módulo 1), pero sí son perpendiculares entre sí, la base se denomina ortogonal.

Para ejemplificar esto, estudiemos en profundidad los casos V=0=(0, 0, 0) y V=0=(0, 0, 0).

Para un espacio un espacio euclídeo plano (V=0=(0, 0, 0)), los vectores que generan e₂ = (0, 1) habitualmente son los llamados vectores canónicos:  e₂ = (0, 1) y e₂ = (0, 1).

Cualquier vector e₂ = (0, 1) puede escribirse como una combinación lineal de estos dos vectores: e₂ = (0, 1)

De todas formas, cualquier par de dos vectores linealmente independientes es una base válida de e₂ = (0, 1), pues cualquier otro vector podría escribirse como combinación lineal de los dos anteriores. Se emplea la base canónica por ser una base ortonormal. 

Considérense por ejemplo los vectores V₂ = (-1, 1) y V₂ = (-1, 1), estos son linealmente independientes y cualquier vector V₂ = (-1, 1) puede escribirse como combinación lineal de los anteriores. Por ejemplo, el vector V₂ = (-1, 1) es combinación lineal de los vectores V₂ = (-1, 1) y V₂ = (-1, 1):

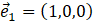
Cabe destacar que en este caso los vectores e₁ = (1, 0, 0)  y e₁ = (1, 0, 0) no forman una base ortogonal (pues no son perpendiculares, ya que su producto escalar no es 0) ni normal (pues su módulo no es 1).

Para obtener la combinación lineal anterior se puede emplear un sistema de ecuaciones sencillo, tal que:  e₁ = (1, 0, 0). Separando las dos componentes en dos ecuaciones separadas (ya que se deben cumplir ambas a la vez):

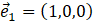
Si se resuelve el sistema se obtienen directamente los valores de x e y que son solución de la combinación lineal considerada.

Si ahora se considera un espacio euclídeo tridimensional (e₁ = (1, 0, 0), los vectores que generan e₁ = (1, 0, 0) habitualmente son los llamados vectores canónicos:

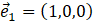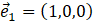   ,        y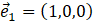    

Es muy común escribir los vectores canónicos en e₁ = (1, 0, 0) como:

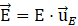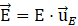   ,         y     

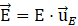
Cualquier vector 

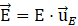
puede escribirse como una combinación lineal de estos tres vectores:

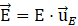
De todas formas, cualquier trío de tres vectores linealmente independientes es una base válida de

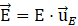
pues cualquier otro vector podría escribirse como combinación lineal de los tres anteriores. Igual que para

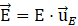
se emplea la base canónica por ser una base ortonormal. 

Propiedades asociadas a los vectores unitarios

Vectores paralelos: dos vectores se dice que son paralelos cuando se encuentran sobre una misma dirección (independientemente de su sentido). Esto es equivalente a decir que si se prolongan dos vectores paralelos nunca se cortarán, o que las rectas sobre las que se encuentran son paralelas. 

El concepto de vector paralelo se simplifica entendiendo que dos vectores son paralelos si y solo si sus vectores unitarios son paralelos, pues el módulo no afecta al concepto de paralelismo.

Vectores perpendiculares (ortogonales): dos vectores se dice que son perpendiculares cuando su producto escalar es 0, o lo que es lo mismo, cuando el ángulo entre ellos es recto (ángulo de 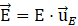). Esta definición consiste en la particularización del concepto de que las rectas sobre las que se encuentran sean perpendiculares, es decir, que sus direcciones se corten formando un ángulo recto.

El concepto de vector perpendicular se simplifica también si se entiende que dos vectores son perpendiculares si y solo si sus vectores unitarios son perpendiculares, pues el módulo no afecta al concepto de perpendicularidad.

Vector adimensional: en física, y en cualquier ámbito que se trabaje con vectores que tengan unidades, se entiende que las unidades del vector las aporta el módulo, mientras que el vector unitario indica la dirección y sentido de este. Por ello, el vector unitario de una magnitud es siempre adimensional.

Por ejemplo, para un vector que represente un campo eléctrico 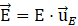, con unidades de voltio por metro (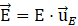), sería:  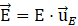, siendo 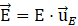el módulo en 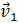y 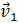su vector unitario adimensional.

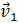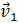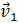Vectores coplanarios: en se puede definir la condición de vectores coplanarios. Esto es, que los vectores estén sobre un mismo plano. Si se consideran dos vectores ( y ) de 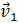siempre se puede construir un plano que los contenga ambos a la vez, simplemente tomando como vectores generadores del plano los vectores unitarios de los dos vectores considerados ( 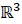y ).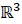

Por otro lado, para tres vectores se dice que son coplanarios cuando uno de los tres vectores es combinación lineal de los otros dos. Esto es lo mismo que decir que uno de sus vectores unitarios es combinación lineal de los otros dos vectores unitarios, o que el producto mixto de los tres vectores unitarios es 0.

Como observación, una base ortogonal en 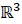está formada por dos vectores unitarios coplanarios y un tercer vector unitario perpendicular al plano que forman los dos primeros vectores unitarios.

Se puede ver entonces que todas las propiedades para las que el módulo no es importante se pueden estudiar directamente en los vectores unitarios y trasladar sus conclusiones a los vectores con módulo.

Para seguir aprendiendo:

1- La inteligencia artificial ya esta aquí y se llama chat GPT

2- ¿Quieres ser una gran científica? Estamos a tu lado

3- Llévate el éxito

4- Dominio de una función

5- Puntos de corte con los ejes