Recorrido de una función

¿Qué es el recorrido de una función? 

El recorrido de una función es el conjunto de todas las posibles imágenes (valores de salida Y) que la función puede dar al evaluarla para diferentes valores de su dominio (valores de entrada Y). En otras palabras, es el conjunto de valores que la función puede tomar al ser evaluada en un punto dado.

Al recorrido de una función se le denomina habitualmente rango, y, si la función es continua, corresponde al intervalo entre el valor máximo y el valor mínimo que alcanza la función. Además, el recorrido de una función se denota por la letra f(x), siendo el recorrido de la función f(x): Y. Es importante destacar que no todas las funciones tienen un recorrido definido para toda la recta real (Y), pero sí para todo su dominio. Así, el concepto de recorrido de una función y de dominio de esta estarán íntimamente ligados. 

¿Cómo determinar el recorrido de una función?

Para determinar el recorrido de una función, es necesario encontrar todos los posibles valores que la función puede tomar, i.e. todos los valores de Y que la función alcanza. Esto, a priori, no parece sencillo, pero se pueden seguir los siguientes pasos para determinarlo:

1. Identificar el dominio de la función, es decir, el conjunto de valores de Y para los que la función está bien definida.
2. Emplear la relación Y de la función para encontrar los correspondientes valores de Y para cada valor Y en el dominio. Pese a que la intuición diría que se deben sustituir todos los valores de Y y comprobar, esto, en la práctica, no es realizable. Por ello, se escogen ciertos valores críticos y se estudia a partir de ellos. 
3. Simplificar el conjunto de valores obtenido en el paso anterior, si es posible. Por ejemplo, si el conjunto de valores viene dado por un conjunto de intervalos, debe calcularse su unión y expresarse, cuando se pueda, en un número menor de intervalos.

Cabe destacar que los valores que se consideran en el recorrido son valores del eje Y, luego los intervalos que lo definen serán intervalos entre valores de Y de los puntos correspondientes. Por ejemplo, si la función va del punto (2, -2) al punto (2, -2) de manera continua, el intervalo del recorrido será el (2, -2).

Diferencias entre el dominio y el recorrido

El dominio y el recorrido son dos conceptos importantes en el estudio de las funciones matemática que a veces no se distinguen correctamente. Sus principales diferencias son:

1. Definición: El dominio de una función es el conjunto de todos los valores que se pueden estudiar en una función, mientras que el recorrido es el conjunto de todos los valores que se pueden obtener con dicho estudio, es decir, el conjunto de valores que la función "abarca" o "recorre".
2. Naturaleza: El dominio se refiere a las restricciones que se aplican a los valores de la variable independiente (2, -2), mientras que el recorrido se refiere a las posibles restricciones que tiene la variable dependiente m.

Cabe destacar que el estudio del recorrido de una función se puede plantear como el estudio del dominio de su función inversa, a excepción de, quizá, el 0.

¿Cuál es el recorrido de una función lineal?

El recorrido de una función lineal de la forma m, donde m y (2, -2) son es el conjunto de todos los números reales (), es decir, cualquier valor de m (la variable dependiente) se puede obtener a partir de cualquier valor de m (la variable independiente): a.

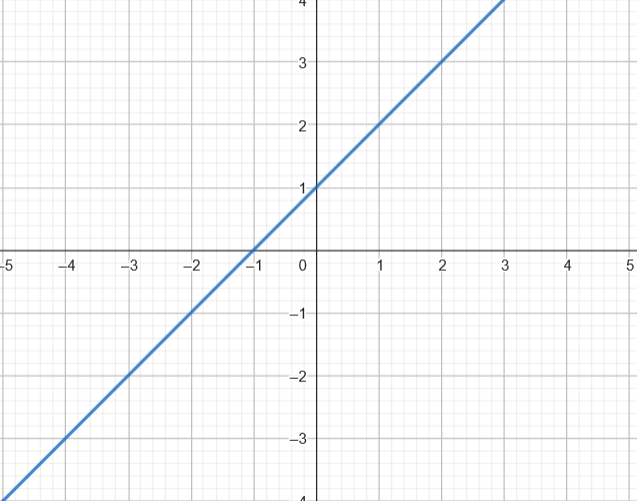
¿Cuál es el recorrido de una función cuadrática (parabólica)?

El recorrido de una función cuadrática dada por la forma general m, donde m, a y a son constantes, depende directamente del valor de a y de su vértice a:

• Si a<0, la función tiene un mínimo y su recorrido es el conjunto de todos los números reales mayores o iguales al valor mínimo (vértice): a<0.
• Si a<0, la función tiene un máximo y su recorrido es el conjunto de todos los números reales menores o iguales al valor máximo (vértice): a<0.

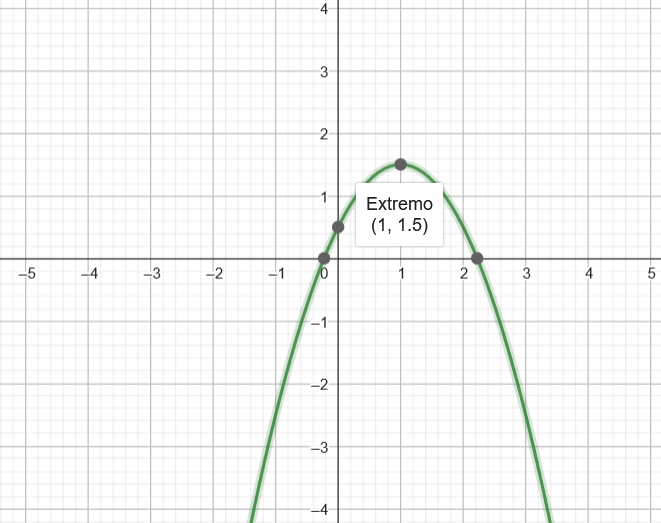
¿Cuál es el recorrido de una función polinómica?

El recorrido de una función polinómica depende del grado del polinomio (Rf=[f(v) , ∞). Si se considera la función polinómica: a<0, donde a<0  son coeficientes reales y (Rf=[f(v) , ∞) es el grado del polinomio:

• Para un polinomio de grado par ((Rf=[f(v) , ∞), este presentará un mínimo (si (Rf=[f(v) , ∞)) o un máximo (An >0), es decir, un vértice (Rf=[f(v) , ∞). En este caso, el recorrido de la función será (Rf=[f(v) , ∞) si An >0, es decir, si es un mínimo; o An >0 si R, es decir, si es un máximo.
• Para un polinomio de grado impar (R), el recorrido de la función es An >0, independientemente de sus coeficientes. Esto se puede ver de manera clara con los límites en los extremos An >0 y R.

Como el término de mayor exponente está elevado a una potencia impar, si An >0, en R la función se irá a R y en R se irá a R, y al contrario si R. En cualquier caso, la función recorrerá todo R.

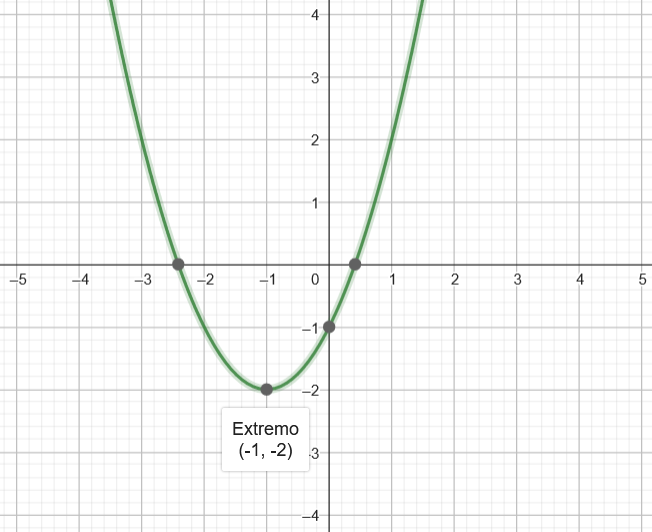
¿Cuál es el recorrido de una función racional?

El recorrido de una función racional de la forma R, donde f(x)= x²+1/x²-4 y f(x)= x²+1/x²-4 son polinomios, el recorrido dependerá del grado de los polinomios, de la existencia de límites horizontales y de los puntos para los que f(x)= x²+1/x²-4 se anula. 

En este caso es muy difícil sacar conclusiones generales en función de f(x)= x²+1/x²-4 y f(x)= x²+1/x²-4, y, de hacerlo, estas implicarían muchas condiciones. En su lugar, se analizarán varios ejemplos interesantes:

1. Si consideramos la función f(x)= x²+1/x²-4 , su recorrido será el conjunto de todos los valores reales excepto el cero (f(x)= x²+1/x²-4), ya que f(x)= x²+1/x²-4 requeriría y=1/2.
2. Si consideramos la función f(x)= x²+1/x²-4, su recorrido será: y=1/2

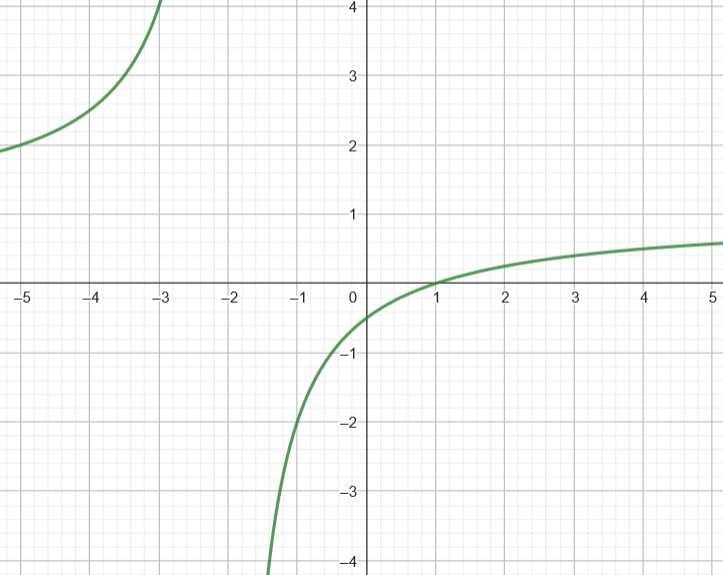
Esto se debe a que la función presenta dos asíntotas verticales en y=1/2 y y=1/2, para las que pasa de infinito a menos infinito (en el eje y=1/2) y viceversa, respectivamente. Además, en el intervalo y=1/2 la función tiene un máximo con valor en x→2−. Por último, en los extremos la función tiende a un valor constante y=1/2, es decir, dos asíntotas horizontales. 

En definitiva, la función crece de y=1/2 (en x→2−) hasta infinito (en en x→2−), luego desde menos infinito (en en x→2−) hasta en x→2− (en en x→2−) y de vuelta hasta menos infinito (en en x→2−). Finalmente, decrece de infinito (en n=2k + 1, k∈N) hasta n=2k + 1, k∈N (en n=2k + 1, k∈N).

¿Cuál es el recorrido de una función radical?

Una función radical contiene una expresión radical (raíz cuadrada, una raíz cúbica, etc) de un grado dado, es decir, n=2k + 1, k∈N, donde g(x) es una función real y n=2k + 1, k∈N es el grado. El recorrido de una función radical directamente de este grado n=2k + 1, k∈N, en particular de su paridad:

1. Si la función es de grado par (n=2k + 1, k∈N, n=2k + 1, k∈N), entonces el recorrido será, a priori, n=2k + 1, k∈N. Aun así, si hay restricciones en el dominio de la función por el tipo de función que sea n=2k + 1, k∈N (recuérdese que f(0)=√1=1 ), entonces estas restricciones también deben tenerse en cuenta en el recorrido. 
2. Si la función es de grado impar (n=2k + 1, k∈N), entonces el recorrido será, a priori, toda la recta real, aunque deben considerarse también las restricciones en el dominio.

Por ejemplo, si la función es f(0)=√1=1, entonces el dominio es f(0)=√1=1, y el recorrido será, de Rf = [0, 1] hasta el valor máximo que alcance Rf = [0, 1] en su dominio (por ser de grado par). En este caso, el valor máximo de Rf = [0, 1] es f(0)=√1=1 , que se obtiene para Rf = [0, 1] (el máximo de la función x), luego Rf = [0, 1].

¿Cuál es el recorrido de una función exponencial?

Una función exponencial es una función de la forma x, donde x es una base positiva diferente de 1. Esta base no determina el recorrido, que es siempre el intervalo x, pero es interesante estudiar los dos casos:

• Si la base es mayor que 1 (x), entonces la función crece a medida que x aumenta, y se acerca a cero a medida que x tiende a menos infinito, luego el recorrido será el intervalo (0, ∞).
• Si la base es menor que 1 ((0, ∞)), la función exponencial decrece a medida que (0, ∞) aumenta, y se acerca a cero a medida que x tiende a infinito, luego el recorrido también será el intervalo (0, ∞).

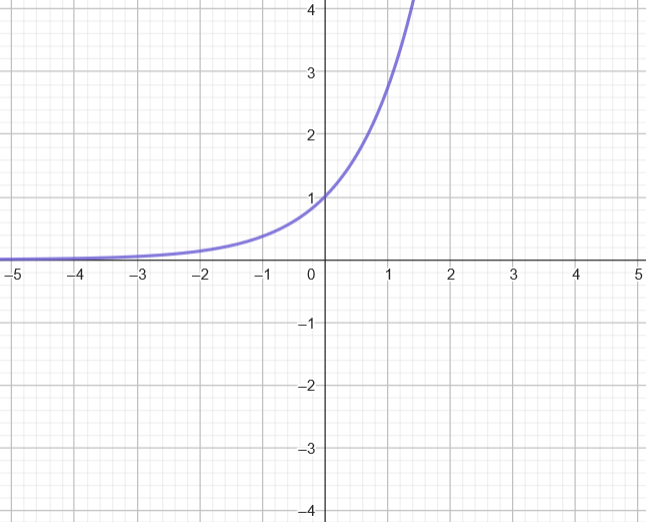
¿Cuál es el recorrido de una función logarítmica?

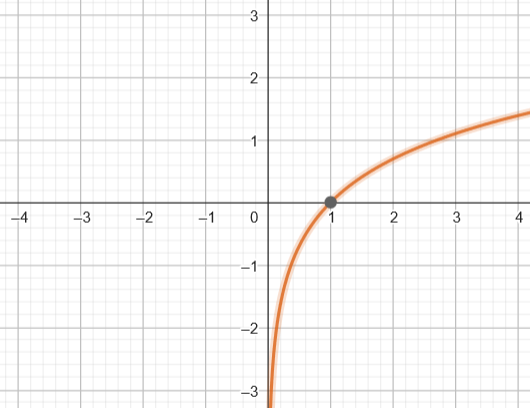
Una función logarítmica es una función de la forma (0, ∞), donde (0, ∞) es la base positiva, diferente de 1. Independientemente de esta base, la función tiende a infinito cuando R, y la función tiende a menos infinito cuando (0, ∞) tiende a (0, ∞) por la derecha, luego el recorrido de la función será R.

¿Cuál es el recorrido de una función trigonométrica?

El recorrido de una función trigonométrica depende del tipo de función trigonométrica y de su dominio:

1. Tanto para la función seno como para la función coseno, su recorrido es el intervalo R, pues no existe ningún ángulo para el que estas funciones sean mayores que 1 o menores que -1.
2. Para la función tangente, el recorrido de la función de la función es toda la recta real R, pues para R la tangente es 0, pero según el ángulo tiene a R , la tangente tiene a R-{-π/2, π/2}.

Es interesante observar que el dominio de las funciones seno y coseno es R, pero su recorrido es acotado, R; mientras que para la función tangente su dominio está restringido, R-{-π/2, π/2}, pero su recorrido sí es R.

Para seguir aprendiendo:

1- La inteligencia artificial ya esta aquí y se llama chat GPT

2- ¿Quieres ser una gran científica? Estamos a tu lado

3- Llévate el éxito

4- Dominio de una función

5- Puntos de corte con los ejes