¿Qué es el producto escalar?

El producto escalar es una operación matemática que se aplica a dos vectores y produce un escalar (un número) como resultado. Esto es, es una operación definida en un espacio vectorial que asocia a cada par de vectores un escalar de manera única, es decir, dos vectores no pueden tener varios productos escalares distintos. No es una función invertible, pues un escalar puede ser producido por productos escalares de distintos vectores.

Pese a que en matemáticas avanzadas se suele representar como <A, B>, en niveles más bajos se representa con un punto: A·B. Es por esta notación que en ocasiones al producto escalar se le denomina “producto punto”, siendo exactamente la misma operación. Debe tenerse clara la diferencia y no debe confundirse el producto escalar entre vectores con el producto habitual entre números (o escalares), pese a representarse ambos por un mismo símbolo (punto). 

¿Cuál es la diferencia entre producto escalar y producto interno?

El producto escalar y el producto interno son términos que se utilizan indistintamente para referirse a la misma operación matemática. Ambos se refieren a la operación que se realiza entre dos vectores para obtener un número escalar como resultado. En términos generales, el término "producto escalar" se utiliza con mayor frecuencia en el ámbito de la matemática, mientras que el término "producto interno" se utiliza más comúnmente en física e ingeniería. Aun así, en algunos contextos matemáticos, se puede utilizar el término "producto interno" para referirse a una forma más general de producto entre vectores, que incluye el producto punto como un caso particular.  Es importante tener en cuenta que, aunque se utilizan indistintamente, el término "producto escalar" y "producto interno" no deben confundirse con el producto vectorial (o producto cruz), que produce un vector como resultado en lugar de un escalar.

¿Cómo se calcula el producto escalar de dos vectores?

El producto escalar se calcula multiplicando las componentes correspondientes de los dos vectores y sumando los resultados. Matemáticamente, si tenemos dos vectores A y B, el producto punto se define para sistemas bidimensionales como: A · B = Ax Bx + Ay By

Y para sistemas tridimensionales como: A · B = Ax Bx + Ay By + Az Bz

Donde Ax, Ay y Az son las componentes del vector A en las direcciones x, y, z, respectivamente, igual para B. Esta definición es, por supuesto, generalizable a más dimensiones. Asimismo, existe una definición del producto escalar que, aunque a priori parece distinta, es análoga. Esta, en lugar de depender de las componentes de los vectores, depende del ángulo que forman y de sus módulos:  A · B = |A| |B| cos(θ),

donde |A| y |B| son los módulos (longitudes) de los vectores y θ es el ángulo entre ellos.

Por ende, existen dos maneras distintas de calcular el producto escalar entre dos vectores, en función de los datos de los que se disponga: Si se tienen las coordenadas de los vectores explícitas, lo más sencillo es multiplicarlas una a una y sumarlas todas. Veamos como ejemplo el producto escalar de los vectores en el espacio tridimensional: A = (2, 3, 4) y B = (-1, 5, 2)

A · B = (2, 3, 4) · (-1, 5, 2) = 2·(-1) + 3·5 + 4·2 = -2 + 15 + 8 = 21

Si se tienen los módulos y el ángulo que forman, se emplea la ecuación anterior para obtener su producto escalar. Veamos por ejemplo el producto escalar de dos vectores, cuyos módulos son |A| = 2, |B| = 3 y el ángulo entre ellos es de θ = 60º:

A · B = |A| |B| cos(θ) = 2 · 3 · cos(60º) = 6 · 1/2 = 3

¿Cómo calcular el producto escalar de tres vectores?

El producto escalar de tres vectores no está definido en el álgebra lineal, pues no tiene sentido plantearlo.  Esto es sencillo de entender, ya que el producto escalar solo se puede definir entre vectores. Así, si se realiza el producto escalar de cualesquiera dos de los tres vectores, se obtendrá un escalar, y luego no tendrá sentido hacer el producto escalar entre el vector que queda y un escalar. Suponiendo que A · B = λ, con λ un escalar (número real), entonces: A · B · C = λ · C = (!!)

En lugar de un producto escalar triple se define el producto mixto, pero solo en espacios de dimensión mayor o igual que 3.

¿Cuáles son las propiedades del producto escalar?

El producto escalar tiene varias propiedades matemáticas importantes que lo hacen una herramienta útil en diferentes contextos. A continuación, se describen algunas de las propiedades más relevantes del producto escalar:

Conmutatividad: El producto escalar es conmutativo, lo que significa que el orden de los vectores no afecta al resultado. En otras palabras, el producto escalar de dos vectores es el mismo independientemente del orden en que se multipliquen:A · B = B · A 

Distributividad: El producto escalar es distributivo respecto a la suma de vectores, lo que significa que el producto escalar de la suma de dos vectores es igual a la suma de los productos escalares: A · (B + C) = A · B + A · C

Asociatividad: El producto escalar no es asociativo, lo que significa que el resultado de multiplicar tres vectores en diferentes órdenes no es necesariamente el mismo. Es decir: (A · B) · C ≠ A · (B · C)

Linealidad: El producto escalar es lineal respecto a un escalar, lo que significa que si se multiplica uno de los vectores por un escalar (número real), el resultado es igual al producto escalar original multiplicado por ese número. Sea λ un escalar: (λ a) · b = λ (a · b)

Módulo o norma de un vector: El producto escalar de un vector consigo mismo devuelve el cuadrado del módulo (norma) del vector. Así, el módulo se define como la raíz cuadrada del producto escalar del vector consigo mismo: |A| = sqrt(A · A)

Habitualmente, en matemáticas se utiliza la notación ||A|| para referirnos a la norma (o módulo) de vectores, mientras que la notación |A| se refiere al valor absoluto de un número. En niveles bajos se suelen usar indistintamente las dos notaciones. 

Desigualdad triangular: el valor absoluto del producto escalar de dos vectores es menor o igual al producto de sus normas, es decir, |A · B| ≤ ||A|| ||B||. La igualdad se cumple si y solo si los vectores son paralelos.

¿Cuándo el producto escalar de dos vectores es 0?

Si dos vectores son ortogonales (perpendiculares), es decir, si tienen un ángulo de 90 grados entre ellos, su producto escalar es igual a cero. Esto se deduce directamente de su fórmula, pues el coseno de 90º es 0, siendo entonces que: A · B = |A| |B| cos (90º) = 0

Esta propiedad es muy útil en matemáticas, física e ingeniería, ya que permite determinar si dos vectores son ortogonales sin tener que calcular el ángulo entre ellos, simplemente haciendo su producto escalar y viendo si este es 0 o no. 

¿Cómo calcular la proyección de un vector sobre otro?

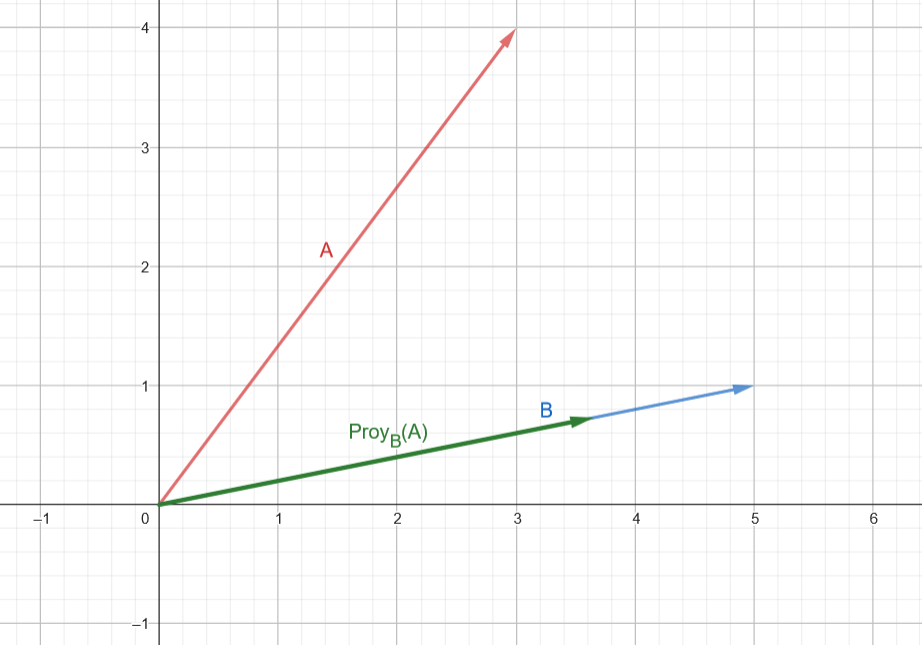
La proyección de un vector A sobre un vector B se define como el vector C que es paralelo a B y cuyo módulo (longitud) es igual a la “sombra” de A sobre B. La proyección de A sobre B se puede calcular utilizando el producto escalar y el vector unitario de la siguiente forma: ProyB(A) = (A · uB) uB

donde uB es el vector unitario asociado al vector B.

En otras palabras, la proyección de A sobre B es igual al producto escalar de A y el vector unitario de B multiplicado de nuevo por dicho vector unitario. La razón por la que se utiliza el vector unitario es porque solo nos interesa la dirección de B y no su módulo.

Por ejemplo, si A = (3, 4) y B = (5, 1), la proyección de A sobre B se puede calcular de la siguiente manera:

uB = B/|B| = (5, 1) / sqrt(5^2 + 1^2 ) = (5/sqrt(26), 1/sqrt(26))

ProyB(A) = ((3, 4) · (5/sqrt(26), 1/sqrt(26))) (5/sqrt(26), 1/sqrt(26)) =

    = (3 · 5/sqrt(26) + 4 · 1/sqrt(26)) (5/sqrt(26), 1/sqrt(26)) = 

    = 19/sqrt(26) (5/sqrt(26), 1/sqrt(26)) = (95/26 , 19/26) 

Por lo tanto, la proyección de A sobre B es (95/26 , 19/26). Este estudio es equivalente para tres dimensiones.

¿Cuál es la interpretación geométrica del producto escalar?

Volviendo a la definición de producto escalar, siendo θ el ángulo entre los vectores: A·B = |A| |B| cos(θ)

El coseno del ángulo θ puede variar de -1 a 1, lo que significa que el producto escalar también puede ser negativo. El signo del producto escalar indica la relación entre los vectores A y B: 

Si el producto escalar es positivo, entonces los vectores apuntan en la misma dirección. 

Si el producto escalar es negativo, entonces los vectores apuntan en direcciones opuestas.

Si el producto escalar es cero, entonces los vectores son perpendiculares

Por otro lado, si dos vectores son paralelos, entonces el ángulo entre ellos es 0º (o 180º) y el coseno de dicho ángulo será 1 (o -1). Así, el producto escalar de dos vectores paralelos es simplemente el producto de sus normas, con un cambio de signo si es necesario porque los vectores apunten en direcciones opuestas: A · B = ± |A| · |B|

Además, el producto escalar también se utiliza para calcular el ángulo entre dos vectores. Si A y B son dos vectores, entonces el ángulo θ entre ellos se puede calcular utilizando la fórmula: cos(θ) = (A · B)/(|A| |B|)

Por ejemplo, si se tienen los vectores A = (2, 3) y B = (-1, 5), entonces los módulos de los vectores son:

|A| = sqrt(2^2 + 3^2) = sqrt(13) 

|B| = sqrt((-1)^2 + 5^2) = sqrt(26)

Para calcular el coseno del ángulo entre los dos vectores se necesita el producto escalar: A · B = (2)·(-1) + (3)·(5) = 13 

Finalmente, el ángulo entre los vectores es: cos(θ) = (A · B) / (|A| |B|) = 13/(sqrt(13) · sqrt(26)) 

Despejando el ángulo como el arco coseno del valor obtenido se llega a que: θ = arccos(13/(sqrt(13) · sqrt(26))) = arccos(1/sqrt(2)) = π/4 = 45º

¿Por qué es importante el producto escalar?

El producto escalar es una operación matemática fundamental que tiene una gran importancia en muchas áreas de la física, la ingeniería, la geometría y la informática, siendo algunas de las aplicaciones más importantes:

Cálculo de la distancia entre dos puntos: el producto escalar se utiliza para calcular la distancia entre dos puntos en un espacio vectorial, pues esta distancia es la norma del vector entre los puntos. Como se ha visto, el módulo es en realidad la raíz cuadrada del producto escalar.

Resolución de sistemas de ecuaciones lineales: si se utilizan matrices y vectores, un sistema de ecuaciones lineales se puede representar como un producto escalar de estos.

Cálculo del ángulo entre dos vectores o dos rectas: como ya se ha visto, el ángulo entre dos vectores se determina directamente a partir de la definición de producto escalar. Asimismo, el ángulo entre dos rectas es directamente el ángulo entre sus vectores directores.

Cálculo de magnitudes escalares en física: muchas magnitudes escalares se definen físicamente como el producto escalar de dos vectores. Por ejemplo, el trabajo mecánico (escalar) se define como el producto escalar del vector de fuerza aplicada y el vector de desplazamiento del objeto.

Análisis de señales: si se considera que cada muestra de una señal es un componente de un vector, entonces el producto escalar de ellos se puede utilizar para calcular el coeficiente de correlación de Pearson, que es una medida de la relación lineal entre las dos señales. Además, también se usa para detectar patrones, identificar señales ocultas y realizar operaciones de filtrado.

Procesamiento de imágenes: En procesamiento de imágenes, el producto escalar se utiliza para calcular el brillo y el contraste de una imagen, y para realizar operaciones de convolución y filtrado. Por ejemplo, para realizar la combinación de dos imágenes, se utiliza el producto escalar de una imagen con una versión girada en 180 grados del filtro. 

Para seguir aprendiendo:

1- La inteligencia artificial ya esta aquí y se llama chat GPT

2- ¿Quieres ser una gran científica? Estamos a tu lado

3- Llévate el éxito

4- Recorrido de una función

5- Puntos de corte con los ejes