Por Resueltoos.com • 14-06-2023 • Matematicas
El número áureo, también conocido como razón áurea o proporción dorada, es un número irracional que se denota por la letra griega phi (φ). Se trata de un numero irracional no periódico con un valor aproximado: 1,6180339887… Esto implica que no se puede expresar como una fracción exacta ni como una repetición periódica de decimales. La definición formal del número áureo es:
La razón áurea es el valor de la proporción que resulta de dividir un segmento en dos partes desiguales, de tal manera que la relación entre el segmento total y la parte más grande sea igual a la relación entre la parte más grande y la parte más pequeña. Esto es, si dividimos una línea en dos partes de manera que la relación entre la parte más grande y la más pequeña sea igual a la relación entre la suma de ambas partes y la parte más grande, entonces esta relación es igual al número áureo.
Matemáticamente, esta proporción se puede expresar como (a+b)/a = a/b, donde "a" es la parte más grande y "b" es la parte más pequeña. De manera concisa, se escribe como: φ = (1 + √5) / 2
El número áureo tiene una gran importancia en las matemáticas, la ciencia y el arte, y ha sido estudiado y utilizado por muchos matemáticos, artistas y diseñadores a lo largo de la historia.
El concepto del número áureo se ha utilizado desde la antigüedad en diversas culturas, pero su descubrimiento y estudio en la forma moderna se le atribuyen al matemático italiano Leonardo Fibonacci, quien lo mencionó por primera vez en su libro Liber Abaci en el año 1202. En su libro, Fibonacci describió un problema que involucraba el crecimiento de una población de conejos y llegó a una progresión aritmética de números naturales que ahora se conoce como la sucesión de Fibonacci. Estos números se obtienen sumando los dos números anteriores de la secuencia, comenzando con 0 y 1: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc.
Fibonacci descubrió que, a medida que los términos de la sucesión de Fibonacci aumentan, la relación entre cada número y su predecesor se aproxima al número áureo. Esto es, si se divide cualquier número en la secuencia por su predecesor, la proporción se acerca cada vez más al número áureo a medida que se avanza en la secuencia:
1/1 = 1
2/1 = 2
3/2 = 1.5
5/3 = 1.66666667
8/5 = 1.6
13/8 = 1.625
21/13 = 1.61538462
34/21 = 1.61904762
55/34 = 1.61764706
89/55 = 1.61818182
Fibonacci no utilizó el término "número áureo", pero se sabe que estudió su relación con la sucesión y reconoció su importancia. De hecho, el nombre fue acuñado más tarde por el matemático alemán Martin Ohm en el siglo XIX, en referencia a la belleza y armonía que el número áureo aporta a la proporción y la estética en la naturaleza y el arte.
Sí, los griegos y romanos conocían el número áureo y lo consideraban un número especial por sus propiedades matemáticas y su belleza estética. Los griegos lo conocían como "la sección dorada" y lo simbolizaban con la letra griega Phi (Φ), mientras que los romanos lo denominaban "el número de oro" y lo representaban con la letra φ. Para los griegos, el número áureo estaba relacionado con el concepto de armonía y proporción en la arquitectura, el arte y la música. Por ejemplo, el Partenón en Atenas, construido en el siglo V a.C., fue diseñado utilizando proporciones que se aproximan al número áureo. Asimismo, la escultura griega clásica se caracteriza por el uso de proporciones áureas para lograr una estética equilibrada y armoniosa.
En cuanto a los romanos, el número áureo era valorado por su utilidad en la medición de objetos y en el diseño de edificios y monumentos públicos. Por ejemplo, el Coliseo de Roma, construido en el siglo I d.C., presenta proporciones que se aproximan al número áureo en su diámetro y altura.
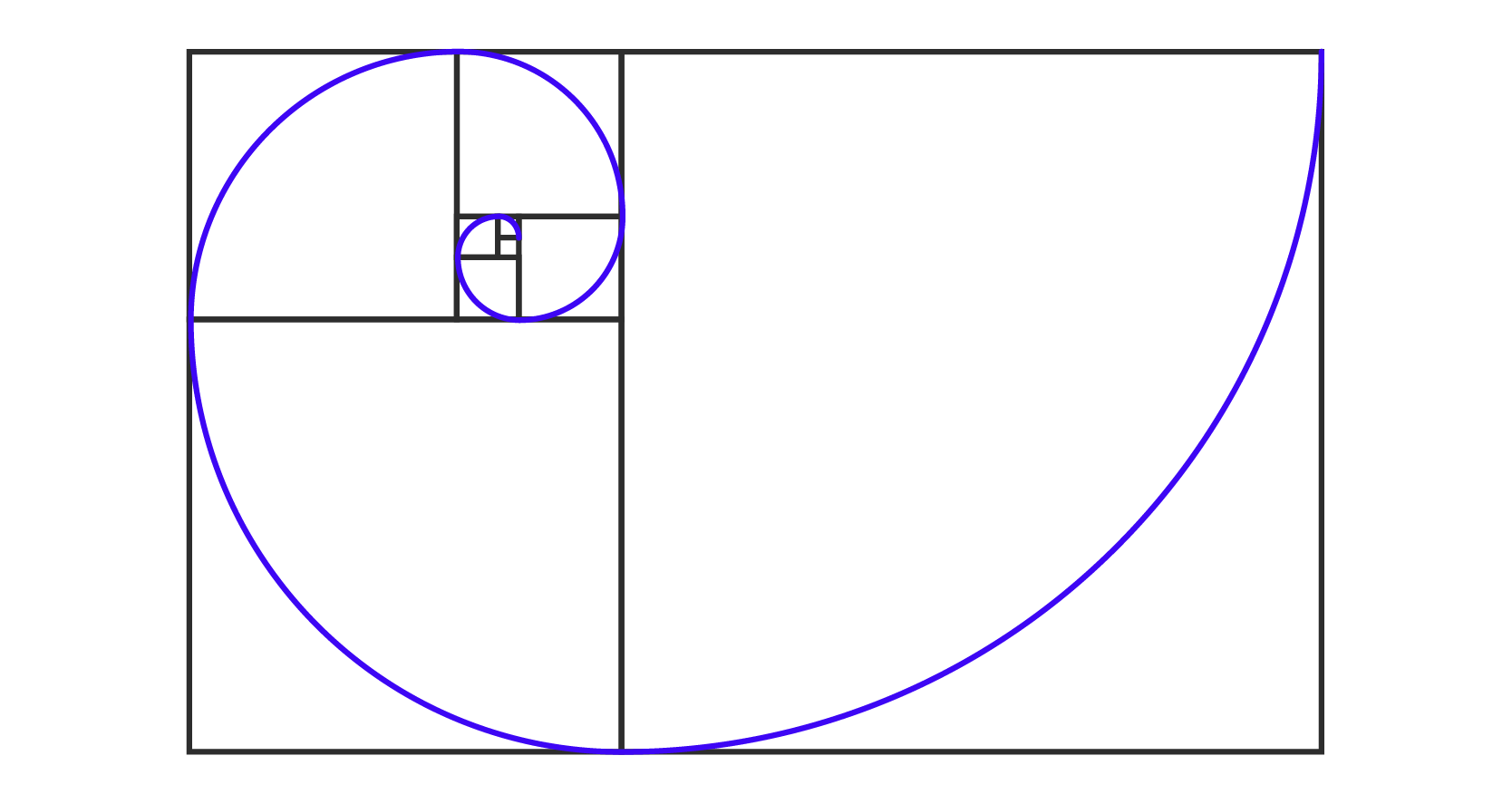
Está claro que sí. De hecho, la razón áurea permite definir dos figuras geométricas planas estéticamente bellas muy importantes y utilizadas en la arquitectura y el diseño desde la antigüedad: el rectángulo áureo y el triángulo de oro. El rectángulo áureo se obtiene si se dibuja un rectángulo con proporciones en las que la relación entre la longitud y la anchura es igual al número áureo. Además, si se añade un cuadrado a uno de los lados más cortos, el rectángulo resultante es un rectángulo más pequeño con las mismas proporciones que el rectángulo original.
El rectángulo áureo se puede construir de la siguiente manera: se comienza con un cuadrado, y se dibuja una diagonal que divide el cuadrado en dos triángulos. Luego se dibuja un segmento de línea que conecta el punto medio de un lado del cuadrado con el punto donde la diagonal corta ese lado. Ese segmento es la longitud del lado del rectángulo, y la anchura es igual a la mitad de esa longitud. Asimismo, el rectángulo áureo también puede ser generado a partir de la sucesión de Fibonacci, construyendo cuadrados sucesivamente de acuerdo con los números de la sucesión, y conectando sus vértices con arcos. El rectángulo que encierra los arcos es un rectángulo áureo. Por otro lado, el triángulo de oro es un triángulo isósceles en el que la relación entre la longitud de la base y la altura es igual al número áureo. Es decir, si llamamos b a la longitud de la base y h a la altura, entonces la relación b/h es igual al número áureo (φ).
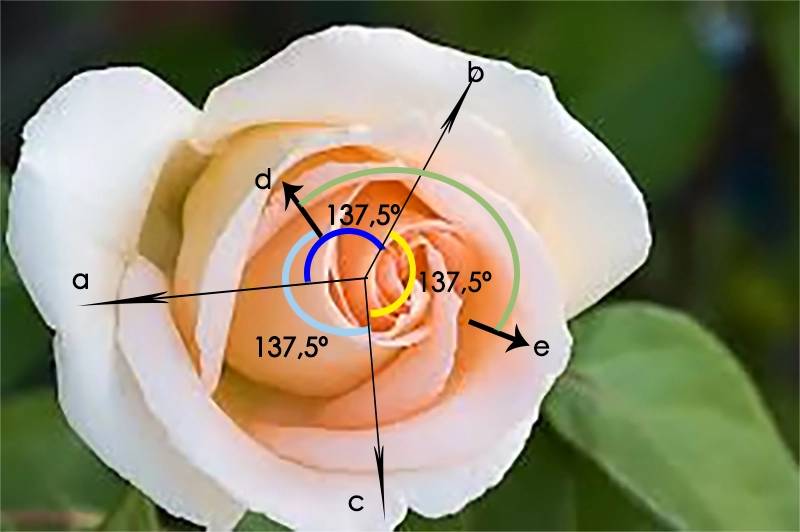
La razón áurea aparece en la naturaleza en diversas formas y patrones, destacando la distribución de hojas y ramas en los árboles. Ésta sigue un patrón que se conoce como "filotaxis", que en muchas especies sigue la secuencia de Fibonacci y, por lo tanto, se aproxima al número áureo. Por ejemplo, en muchos árboles, una rama crece en un ángulo de alrededor de 137,5 grados respecto a la rama anterior, lo que corresponde a la proporción del número áureo. De manera similar, en las flores y frutos la disposición de los pétalos y la ubicación de los pistilos y estambres siguen patrones que se aproximan al número áureo. Por ejemplo, en la margarita, la disposición de los pétalos sigue la secuencia de Fibonacci, y la disposición de las semillas en algunas frutas, como la piña y el ananá, sigue patrones similares.
Además, las conchas de algunos moluscos presentan una espiral que se forma en la parte exterior sigue una curva que se aproxima a la espiral áurea, pues la curva se forma alrededor de un punto central mientras se va alejando progresivamente en la misma proporción que el número áureo. Por otro lado, en la formación de galaxias se ha observado una disposición de estrellas y gases que sigue una estructura espiral que se aproxima a la espiral áurea, sugiriendo que la razón áurea puede estar presente en la distribución de la materia en el universo.
El número áureo ha sido utilizado en la cultura y el arte desde la antigüedad:
Arquitectura: además de los griegos y romanos, muchas catedrales medievales y edificios renacentistas también se diseñaron utilizando la proporción áurea.
Arte: el pintor renacentista Leonardo da Vinci utilizó la proporción áurea en muchas de sus obras, incluyendo la Mona Lisa. También se ha encontrado que la proporción áurea está presente en muchas obras de arte clásico, como las esculturas griegas y las pinturas de la Edad de Oro holandesa.
Música: se ha descubierto que muchas piezas musicales clásicas, como las obras de Bach y Mozart, contienen patrones de proporciones basados en el número áureo.
Literatura: el escritor francés Georges Perec escribió una novela llamada La Disparition (La Desaparición) que no contiene la letra "e". El libro se estructura en capítulos de diferentes longitudes, cuyas proporciones están basadas en el número áureo.
Logotipos: muchos de los logotipos que estamos acostumbrados a ver en marcas archiconocidas hacen un extenso uso de la razón áurea, como Apple, Nike o McDonalds.
A día de hoy, el número áureo se sigue utilizando en muchos campos, aunque su uso ya no es exclusivamente estético:
1- La inteligencia artificial chat GPT
2- ¿Quieres ser una gran científica?
5- Puntos de corte con los ejes
Dominio de una función
01-06-2023
Recorrido de una función
02-03-2023
Puntos de corte con los ejes
05-05-2023
Puntos de corte de funciones racionales, logarítmicas, trigonométricas
02-03-2023
