Consigue 5 días de prueba gratuita registrándote ahora
En nuestro e-book gratuito, encontrarás estrategias probadas que ayudarán a tu hijo a mejorar sus hábitos de estudio. ¡Transforma su manera de estudiar hoy mismo!

Resueltoos.com Física y química
03-03-2025
Los factores de conversión son operaciones matemáticas que se utilizan para cambiar de una unidad de medida a otra, o para calcular la equivalencia entre los múltiplos y submúltiplos de una determinada unidad de medida. Así, conociendo la equivalencia entre dos unidades de medida, se puede pasar de una a otra con un simple procedimiento matemático. Se expresan como fracciones, donde el numerador representa la unidad de destino (la unidad a la que se quiere llegar) y el denominador representa la unidad de origen (la unidad inicial).
El procedimiento para pasar de una unidad a otra utilizando factores de conversión es el siguiente:
Encontrar la relación entre las unidades de medida: tras identificar las unidades de medida, se debe encontrar la relación matemática entre ellas. Por ejemplo, para convertir de kilómetros a millas, sabemos que 1 kilómetro es aproximadamente igual a 0,621371 millas.
Calcula el factor de conversión: El factor de conversión es el número que se obtiene al calcular la relación entre ambas unidades. Así, el factor de conversión es el resultado de la fracción que tiene por numerador la magnitud que se quiere obtener y por denominador la magnitud de partida. En este caso, el factor de conversión sería 0,621371 / 1.
Aplicar el factor de conversión: Multiplica la cantidad que deseas convertir por el factor de conversión obtenido. Aplicando esto al ejemplo anterior, si estás convirtiendo kilómetros a millas y tienes 10 kilómetros, se debe multiplicar 10 km por 0,621371 / 1 para obtener el resultado en millas.
También es posible utilizar factores de conversión para calcular la transición entre submúltiplos y múltiplos de la misma magnitud, como pasar de centímetros a metros, de gramos a kilogramos, etc., siempre y cuando se sepa la relación entre ambos.

A lo largo de la historia, se han desarrollado sistemas de unidades en diferentes partes del mundo muy distintas entre sí. Cada cultura y sociedad tenía sus propios sistemas de medida basados en objetos o referencias locales, como la barra de Aragón o el Talento griego. Con el tiempo, estos sistemas de medidas locales comenzaron a suponer un gran problema de entendimiento entre personas de diferentes regiones: Imagina que una modista inglesa encargaba tela a una tienda en España, ¿cómo podría saber cuánta tela necesitaba la modista inglesa si allí la unidad de longitud era el “pie” mientras que en España se utilizaba la “vara”? De esta forma, la necesidad de creación de un sistema universal de medida que permitiera relacionar todos los demás se volvió de vital importancia.
Esta necesidad fue resuelta en el siglo XVIII durante la Revolución Francesa, con la introducción del sistema métrico, el cual impuso un sistema decimal basado en el kilogramo y el metro. En el siglo XX, la Conferencia General de Pesas y Medidas (CGPM) introdujo el Sistema Internacional de Unidades (conocido originalmente en francés como el Système International d'unités o SI), el cual incluía siete “unidades fundamentales”, que eran el metro, el kilogramo, el segundo, el amperio, el kelvin, el mol y la candela, además de 22 unidades adicionales que se derivaban de estas unidades fundamentales.
Una vez estandarizadas las unidades de medida, fue realmente sencillo pasar de un sistema de medida a otro mediante los llamados “factores de conversión”, que, hoy en día, son una herramienta fundamental para relacionar diferentes unidades de medida, así como para pasar de un múltiplo a otro de una misma magnitud.
El Sistema Internacional de Unidades (SI) es el sistema de unidades de medida internacionalmente aceptado y utilizado en todo el mundo para expresar magnitudes físicas de manera estandarizada y coherente. El SI consta de siete unidades básicas, que son:
Metro (m): El metro es la unidad fundamental de longitud. Originalmente, fue definido en términos del tamaño de la Tierra, mientras que ahora se define como la distancia que recorre la luz en el vacío durante un intervalo de tiempo de 1/299792458 segundos.
Kilogramo (kg): El kilogramo es la unidad fundamental de masa. Pese a que durante muchos años se definió como la masa del prototipo internacional del kilogramo, conocido como el "Gran K", actualmente se define en base a la constante de Planck, utilizando la balanza de Kibble (también conocida como balanza de Watt).
Segundo (s): El segundo es la unidad básica para medir intervalos de tiempo y está definido por la vibración de átomos de cesio en una transición específica.
Amperio (A): El amperio (o ampere) es la unidad fundamental de corriente eléctrica y representa la cantidad de carga eléctrica que fluye por un conductor en un segundo.
Kelvin (K): El kelvin, que no “grado” kelvin, es la unidad fundamental de temperatura termodinámica. Representa la temperatura termodinámica de un sistema y está basado en la temperatura del punto triple del agua y en el cero absoluto (la temperatura mínima permitida termodinámicamente). Por ello, la temperatura termodinámica del punto triple del agua es igual a 273,16 kelvin exactamente y el cero absoluto se encuentra a 0 kelvin.
Mol (mol): El mol es la unidad fundamental de cantidad de sustancia. Representa la cantidad de sustancia de un sistema que contiene tantas partículas elementales (como átomos, moléculas o iones) como átomos hay en 12 gramos de carbono-12, una forma particular de carbono. Esta cantidad es aproximadamente igual a 6,02214076*10^23 partículas y se conoce como el número de Avogadro.
Candela (cd): La candela es la unidad fundamental de intensidad luminosa y representa la cantidad de luz emitida por una fuente en una dirección específica. Originalmente, se definía en términos de una fuente luminosa específica, pero actualmente se basa en una constante física relacionada con la radiación electromagnética.
Además de las unidades fundamentales, existen unidades derivadas del SI que se originan a partir de las primeras mediante combinaciones y relaciones matemáticas. Algunos ejemplos de unidades derivadas son:
Newton (N): Es la unidad derivada de fuerza. En unidades fundamentales se puede expresar como kg * m * s¯².
Pascal (Pa): Es la unidad derivada de presión. En unidades fundamentales se puede expresar como m¯¹ * kg * s¯².
Julio (J): Es la unidad derivada de trabajo. En unidades fundamentales se puedes expresar como m² * kg * s¯².
Culombio (C): Es la unidad fundamental de carga eléctrica. En unidades fundamentales se puede expresar como A*s.
Es importante distinguir las unidades derivadas de los múltiplos y submúltiplos de las unidades fundamentales, que se denotan con prefijos como kilo-, mega-, giga-, centi-, mili-, micro-, nano-, entre otros.
El sistema decimal es un sistema numérico basado en la base 10, lo que significa que está formado por diez dígitos distintos, desde el 0 hasta el 9. Este sistema es ampliamente utilizado en todo el mundo y es la base de nuestro sistema numérico cotidiano. En este sistema, cada posición en un número representa una potencia de 10, esto es, el primer dígito empezando por la derecha representa una potencia 10^0, el segundo una potencia 10¹, el tercero una potencia 10², y así sucesivamente. Por ejemplo, para el número 793, el 3 está en la posición de las unidades y representa 3 * 1 = 3, el 9 está en la posición de las decenas y representa 9 * 10 = 90 y el 7 está en la posición de las centenas y representa 7 * 10² = 700.
Existe una gran variedad de magnitudes que utilizan este sistema, como la longitud, la masa, la corriente eléctrica, o la energía.
La transición entre submúltiplos (fracciones menores a 1) y múltiplos (números enteros mayores a 1) en el sistema decimal implica multiplicar o dividir por potencias de 10. De esta forma, si se quiere pasar de metros (m) a kilómetros (km), se debe dividir entre 10^3, mientras que, si se quiere hacer la operación inversa, se debe multiplicar por 10³.
_1698673034.webp)
El sistema sexagesimal es un sistema de numeración de base 60. Esto significa que tiene 60 dígitos diferentes antes de volver a empezar con un dígito adicional, similar al sistema decimal que usamos en la vida cotidiana, que se basa en la base 10. En geometría y trigonometría, el sistema sexagesimal se utiliza para medir ángulos. En este sistema, un ángulo completo equivale a 360 grados, donde cada grado se subdivide en 60 minutos (') y cada minuto se subdivide en 60 segundos ("). Así, la notación para un ángulo en grados, minutos y segundos se ve de la siguiente manera:
Ángulo = gradosᵒ minutos’ segundos’’
Esto significa que 30ᵒ15’ es igual a 30 grados y 15 minutos.
Otra magnitud importante que se mide mediante el sistema sexagesimal es el tiempo, donde un día se divide en 24 horas, cada hora se divide en 60 minutos, y cada minuto se divide en 60 segundos.
Como se ha explicado anteriormente, la transición entre submúltiplos (fracciones menores a 1) y múltiplos (números enteros mayores a 1) en el sistema sexagesimal, implica multiplicar o dividir por potencias de 60. Por consiguiente, si se quiere pasar de horas a segundos, se deberá multiplicar por 60^2, mientras que, si se quiere calcular la operación inversa, se debe dividir entre 60^2.
Descubre Resueltoos, la plataforma educativa líder en la transformación de la enseñanza de las matemáticas. Nuestra propuesta beneficia tanto a padres como a estudiantes de manera excepcional. Los padres confían plenamente en Resueltoos gracias a nuestros tutores virtuales altamente capacitados y seguimiento personalizado, lo que garantiza un éxito académico sólido para sus hijos. Por su parte, los estudiantes se entusiasman con Resueltoos debido a su enfoque interactivo y divertido con juegos educativos que hacen que las matemáticas sean fascinantes. Cambiamos las matemáticas de un obstáculo a una habilidad crucial que abre puertas hacia un futuro prometedor. ¡Suscríbete ahora y prepárate para un viaje educativo excepcional!
2- ¿Quieres ser una gran científica?
5- Puntos de corte con los ejes
6- ¿Cuáles son las leyes de los gases?
Resueltoos
03-03-2025

Resueltoos.com
El movimiento circular se refiere a cualquier movimiento en el cual un objeto se mueve alrededor de un punto central en una trayectoria circular
Resueltoos
03-03-2025
Resueltoos.com
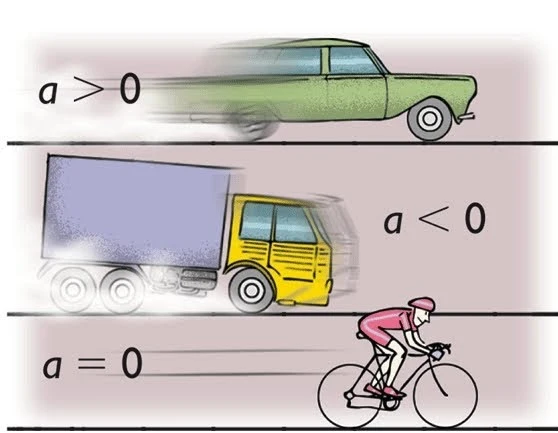
Un movimiento rectilineo es aquel en el que un objeto se mueve en linea recta, es decir, su trayectoria no presenta curvas ni cambios de direccion
Resueltoos
03-03-2025
Resueltoos.com
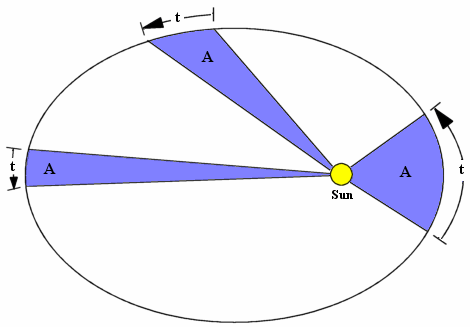
Las leyes de Kepler son tres principios empíricos que describen el movimiento de los planetas alrededor del Sol
Descubre nuestro e-book repleto de secretos para aprobar cada examen

Este sitio utiliza diferentes tipos de cookies. Puedes obtener detalles sobre todas las cookies utilizadas en este sitio haciendo clic a continuación en cada categoría de cookies. Las cookies estrictamente necesarias están siempre activadas, pero puedes gestionar tus preferencias dando tu consentimiento para el uso de cookies adicionales como se describe en nuestra Política de Cookies
Estas cookies son necesarias para que el sitio web funcione y no se pueden desactivar en nuestros sistemas. Por lo general, solo se configuran en respuesta a sus acciones realizadas al solicitar servicios, como establecer sus preferencias de privacidad, iniciar sesión o completar formularios. Puede configurar su navegador para bloquear o alertar sobre estas cookies, pero algunas áreas del sitio no funcionarán. Estas cookies no almacenan ninguna información de identificación personal.
Estas cookies nos permiten contar las visitas y fuentes de tráfico para poder evaluar el rendimiento de nuestro sitio y mejorarlo. Nos ayudan a saber qué páginas son las más o las menos visitadas, y cómo los visitantes navegan por el sitio. Toda la información que recogen estas cookies es agregada y, por lo tanto, es anónima. Si no permite utilizar estas cookies, no sabremos cuándo visitó nuestro sitio y no podremos evaluar si funcionó correctamente.
Estas cookies permiten recordar tus preferencias y configuraciones para mejorar tu experiencia en el sitio web. Gracias a ellas, el sitio puede recordar tus elecciones, como el idioma, región o configuraciones personalizadas. Si no permites estas cookies, algunas partes del sitio pueden no funcionar correctamente.
Estas cookies nos permiten gestionar, de la forma más eficaz posible, de los espacios publicitarios que, en su caso, se hayan incluido en el sitio web de Resueltoos.