Por Resueltoos.com • 21-09-2023 • Matematicas
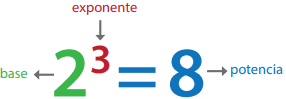
Una potencia es una expresión que se utiliza para denotar la multiplicación repetida de un número por sí mismo un número determinado de veces. Se representa de la siguiente manera: a^n
Donde “a” es la base (número que se multiplica por sí mismo) y “n” es el exponente (número que indica cuántas veces se multiplica la base por sí misma). Un ejemplo sencillo de potencia es 2^4, lo que se lee como “dos elevado a la cuarta potencia” y significa 2*2*2*2=16.
El concepto fundamental de los exponentes tiene su origen en la antigua Grecia, donde Euclides empleó el término "potencia" para indicar cuántas veces un número debía multiplicarse por sí mismo. En el siglo XIV, Nicolás Oresme también utilizó números para representar el concepto de potencias, aunque no se empleó notación simbólica en ese momento.
La introducción de la notación de números elevados para representar exponentes se produjo en el siglo XVII. Hérigone utilizó símbolos como "a3" para representar "a por a por a", aunque no elevó el exponente. David Hume, en 1636, introdujo el uso de números romanos (como III o IX) para indicar exponentes. Finalmente, en 1637, René Descartes fue el primero en emplear exponentes positivos de la manera moderna.
Los exponentes con valores negativos en la notación exponencial aparecieron gracias a Isaac Newton en 1676. Aunque Nicolás Oresme ya había utilizado exponentes fraccionarios en el siglo XIV, no se empleó la notación moderna hasta la contribución de Newton en 1676. El uso de exponentes y la notación científica experimentaron un aumento en el siglo XIX. En esta época, se volvió común representar números grandes mediante la notación científica, como, por ejemplo, expresar el número 8.900.000.000 como 8.9 por 10 elevado a la novena potencia. Este cambio en la notación se debió en gran medida a las investigaciones astronómicas y microscópicas que requerían la manipulación de números extremadamente grandes o pequeños.
La relación entre las potencias y las raíces radica en el hecho de que son operaciones opuestas entre sí. Por un lado, si se tiene a^n, la raíz n-ésima de a^n es igual a “a”. Esto se expresa como ⁿ√a^n=a. Por otro lado, si se tiene ⁿ√a, al elevarlo a la n-ésima potencia se obtiene “a”. Esto se expresa como (ⁿ√a)^n=a.
Las potencias tienen muchas propiedades interesantes que facilitan los cálculos y las manipulaciones matemáticas. Algunas de las propiedades más importantes incluyen:
Producto de potencias de la misma base: Si se tiene a^n*a^m, donde “a” es la misma base, es posible sumar los exponentes para obtener a^(n+m).
Cociente de potencias de la misma base: Si se tiene a^n/a^m, donde “a” es la misma base, se pueden restar los exponentes para obtener a^(n-m).
Potencia de una potencia: Si se tiene (a^n)^m, es posible multiplicar los exponentes para obtener a^(n*m).
Potencia de un producto: Si se tiene (a*b)^n, es posible distribuir el exponente par obtener a^n*a^m.
Potencia de un cociente: De forma análoga al caso anterior, si se tiene (a/b)^n, es posible distribuir el exponente para obtener a^n/b^n.
Potencia de un exponente negativo: Si se tiene a^(-n), es posible reescribir esta expresión en forma fraccionaria como la unidad partido de “a” elevado a “n” positivo, es decir, 1/a^n.
Un polinomio es una expresión algebraica que se forma combinando términos algebraicos de una o más variables, donde cada término consiste en el producto de una constante (llamada coeficiente) y una potencia de una variable.
La forma general de un polinomio en una variable “x” es: P(x) = a_n x^n + a_(n-1) x^(n-1) + … + a_1 x +a_0
Donde “x” es la variable independiente, a_n, a_(n-1),…, a_1, a_0 son los coeficientes del polinomio y “n” es un número entero no negativo que representa el grado del polinomio. Cada término del polinomio es una potencia de “x”. Esta relación se vuelve más clara cuando observamos un término individual de un polinomio, como 3x². En este término, el coeficiente es 3, y x² es una potencia de “x” con exponente 2. Por lo tanto, los polinomios son una forma de combinar y manipular potencias de variables (en este caso “x”) mediante la multiplicación y la suma.
Una serie geométrica es una secuencia infinita de términos que se obtienen multiplicando un término inicial por una constante llamada razón. La serie geométrica es un caso especial de expansión de una función en serie de potencias, y se utiliza para representar una función como una suma infinita de potencias de una variable. Se ve de la siguiente forma: a + ar + ar^2 + ar^3 + ar^4 + …
Donde “a” es el primer término de la serie, también conocido como término inicial, y “r” es la razón común entre los términos consecutivos. La relación entre la serie geométrica y las potencias se vuelve más evidente cuando consideramos el caso especial en el que a=1. En este caso, la serie geométrica se reduce a: 1 + r + r^2 + r^3 + r^4 + …
El comportamiento de los términos de la serie depende del valor que tome la razón. Si |r| es mayor o igual a 1, los términos de la serie se incrementan en magnitud, de manera que la serie diverge y no tiene un valor finito. Sin embargo, si |r| es menor que 1, los términos decrecen y se acercan a cero en el límite. En tal caso, la serie converge y se puede calcular su suma mediante la siguiente fórmula: S = a/(1-r)
Las potencias con exponentes irracionales son una extensión fascinante de las potencias en matemáticas. A diferencia de los exponentes enteros o fraccionarios, los exponentes irracionales son números que no pueden expresarse como una fracción de números enteros. Obtener el resultado numérico para este tipo de potencias se vuelve en muchos casos una ardua tarea. Para ciertas funciones, como la función exponencial e^x, es posible expresar potencias con exponentes irracionales como series de potencias. Por ejemplo, e^x se puede expandir en una serie de Taylor, lo que permite calcularlo para exponentes irracionales.
Los números complejos se representan generalmente en la forma a+bi, donde “a” y “b” son números reales e “i” es la unidad imaginaria, que satisface i^2=-1. Supongamos ahora que se tiene un número complejo “z” en la forma z=a+bi y se quiere calcular z^n, siendo “n” un número entero. Existen dos opciones: aplicar propiedades de las potencias directamente, esto es, partiendo de: z^n = (a+bi)^n, se expande esta expresión y se simplifican los términos siguiendo las propiedades antes mencionadas.
La segunda opción es utilizar la fórmula de Moivre, la cual establece que: (r (cosθ + i*sinθ))^n = r^n (cos(nθ) + i*sin(nθ)), donde “r” es el módulo del número complejo “z”, r= √a²+b², y θ es el argumento del número complejo “z”.
Las potencias son un concepto matemático fundamental con una amplia variedad de aplicaciones. Algunas de sus principales utilidades son las siguientes:
Cálculo de áreas y volúmenes: En geometría, las potencias se utilizan para calcular áreas de figuras planas y volúmenes de objetos tridimensionales. Por ejemplo, el área de un cuadrado de lado “a” se expresa como a^2 y el volumen de un cubo con arista “a” es a^3.
Resolución de ecuaciones algebraicas: Las potencias son esenciales para resolver ecuaciones algebraicas, ya que permiten simplificar expresiones y encontrar soluciones. Por ejemplo, para resolver x^2=16, es necesario usar las propiedades de las potencias para obtener x=+4 y x=-4.
Notación científica: En ciencia, la notación científica utiliza potencias para expresar números extremadamente grandes o pequeños de manera más compacta y comprensible. Un ejemplo de ello es la velocidad de la luz en el vacío, que se expresa como 3*10^8 metros por segundo.
El Teorema del Binomio es un resultado fundamental en álgebra que establece cómo expandir una expresión de la forma (a+b)^n, donde “a” y “b” son números o expresiones algebraicas, y “n” es un número entero no negativo.
La expresión general del Teorema del Binomio es la siguiente: (a+b)^n = C_0 a^n b^0 + C_1 a^(n-1) b^1 + C_2 a^(n-2) b^2 + … C_n a^0 b^n
Donde C_k representa el coeficiente binomial, que se calcula como C_k=n!/(k!(n-k)!). Aquí, n! es el factorial de “n”, esto es, el producto de todos los enteros positivos desde 1 hasta “n”. Un ejemplo sencillo en el que se puede aplicar este teorema es en el cálculo de (x+2)^3. En este caso, a=x, b=2 y n=3, por lo que, aplicando el Teorema del Binomio: (x+2)^3 = C_0 x^3 2^0 + C_1 x^2 2^1 + C_2 x^1 2^2 + C_3 x^0 2^3, Así, tras calcular los coeficientes binomiales con la expresión anteriormente explicada se obtiene: (x+2)^3 = x^3 +6x^2 + 12x + 8
Una forma más sencilla de obtener los coeficientes binomiales es hacer uso del Triángulo de Pascal, el cual consiste en una disposición triangular de los coeficientes binomiales ordenados.
Descubre Resueltoos, la plataforma educativa que revoluciona el aprendizaje de matemáticas. Beneficia a padres y alumnos por igual. Padres confían en nuestros tutores virtuales y seguimiento personalizado. Los estudiantes aman Resueltoos por su enfoque divertido con juegos interactivos y accesibilidad en cualquier lugar. Las matemáticas dejan de ser una barrera y se convierten en una herramienta para un futuro brillante. Suscríbete y prepárate para un viaje educativo excepcional.
2- ¿Quieres ser una gran científica?
3- Problema de los 3 servicios
5- Puntos de corte con los ejes
Dominio de una función
01-06-2023
Recorrido de una función
02-03-2023
Puntos de corte con los ejes
05-05-2023
Puntos de corte de funciones racionales, logarítmicas, trigonométricas
02-03-2023
